どうもgive-keyです。
今回はハーモニックパターンを解説していきます。
ハーモニックパターンとは、調和された形を形成することからそう呼ばれています。
調和とは何なのかと言いますと、 自然界に存在する比率が存在するように、チャートパターンにもそれに準ずる比率が存在するという着目点から生まれた分析手法なんですね。
例えば、花びらの数は、フィボナッチ数で構成されている事が分かります。 googleで「フィボナッチ 花びら」と検索すると出てくると思いますので気になる方は調べてみて下さい。
更にその花びらの配置はとある規則に沿っているんです。
その規則とは、皆さんお馴染みの「黄金比」というものです。
この黄金比はフィボナッチ数列から導き出されており、人間が最も調和された比率、最も安定的で美しいと感じる比率と言われています。
その黄金比が実際のチャートパターンを描く際に、投資家たちが無意識に感じる調和された形をトレードの根拠にしていれば、パターンとして現れるのではないかと考えたわけですね。
これをハーモニックパターンと呼んでいます。
そしてこのハーモニックパターンの最大の活躍タイミングは、実は逆張りトレードなんです。
正確にいうと、とある地点で反転するラインやゾーンを先取りできるというものです。
では、実際にこのハーモニックパターンと、それの根拠となるフィボナッチ数列の簡単な解説、メリットとデメリットを解説していきます。
ハーモニックパターンの背景
欧米の方を中心に人気のあるフィボナッチ数列を使用した分析手法です。
日本の方にはあまり馴染みがない手法と言えますが、少し難しいといった印象が強いそうです。
このハーモニックパターンを理解する前提条件として、フィボナッチ数列がどの様にチャート上で機能しているか理解している必要があります。
詳しいフィボナッチ数列については、また別の記事で紹介します。
ここでは簡単にフィボナッチ数列について解説していきます。
フィボナッチ比率
まず、フィボナッチ比率を解説する前にフィボナッチ数列について軽く触れておく必要があるので、例を出しながら説明していきます。
フィボナッチ数列とは、数字の0,1から始まり、次の数字は前回の2つの数字を常に合計し続ける数列のことを指します。
0,1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597…
このように0+1=1、1+1=2、1+2=3と規則正しく加算してく数列なんです。
そしてフィボナッチ比率とは、数列内の1つの数値と数列内の別の数値で割った比率を指しています。

例えば、0.1.1.2と並んでいるフィボナッチ数列の1.1を選んで割って比率を出すと100%となります。
また、1.2を選んで割って比率を出すと、200%と50%という比率が導き出せると思います。
この比率がフィボナッチ数列です。
では、他のフィボナッチ数列も見てみましょう。
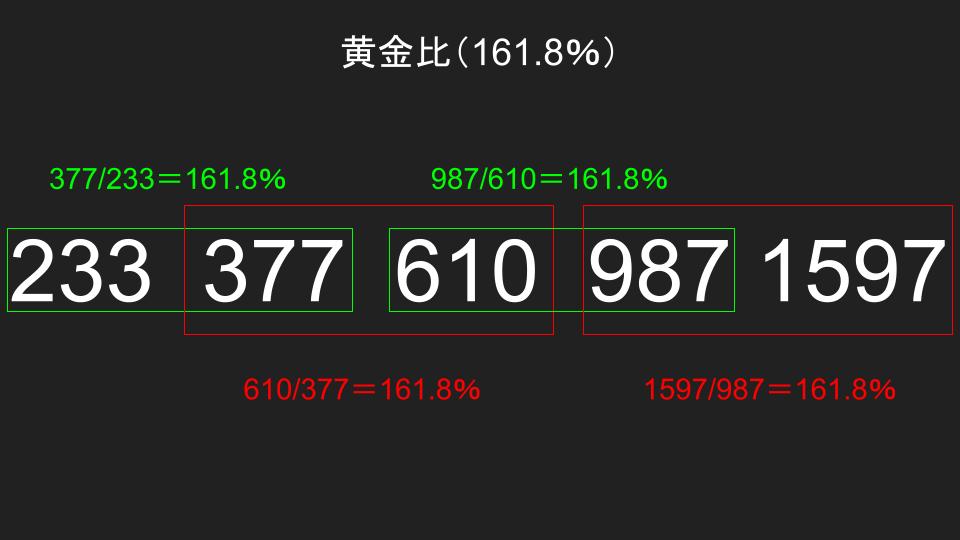
次は黄金比と呼ばれるものです。
ある数字から前回の数字で割った比率になります。
フィボナッチ数列の項を進めていくと、実はこの161.8%に収束していきます。
この161.8%という比率が最も自然界の中で美しいとされている比率になる訳です。
ゆえに私たちは無意識にこの比率を意識していることになります。
更に次を見てみましょう。

この61.8%とは、黄金比の計算とは反対で、前回の数字から次の数字で割った比率になります。
実はこれも61.8%に収束していきます。
この様にフィボナッチ比率は規則性を持っています。
他の規則性も確認しましょう。

この261.8%は隣り合う整数ではなく、一つ飛び越えた整数を使って比率を導き出したものです。

38.2%は、261.8%で使用した整数の逆数となります。
以上、4つの例を出しましたが、もう分かる通りフィボナッチ比にはある法則性が存在します。
それは、
フィボナッチ比は、フィボナッチ数列全体で一定である という事です。
つまり、ハーモニックパターンはフィボナッチ数列を基にしているので、このフィボナッチ比は必ず意識される比率となります。
実際にハーモニックパターン内で最も使用される比率は
38.2%、50%、61.8%、161.8%、261.8%、361.8%
また、61.8と161.8には√と∜の値も意識されます。
61.8の√の78.6%、∜の88.6%
161.8の√の127.2%、∜の113%
これらはあくまでも補助的に覚える程度にしておくといいでしょう。
金融市場におけるフィボナッチ
では、フィボナッチ数列やフィボナッチ比率の概要を捉えたところで、今度は金融市場におけるフィボナッチを適用するにはどうしたらいいのか説明します。
チャートでは基本的に縦軸で見る価格変動の比率を測定します。
ある価格から他の価格までの変動との関係性をフィボナッチ比率に当てはめてサイズを計算します。
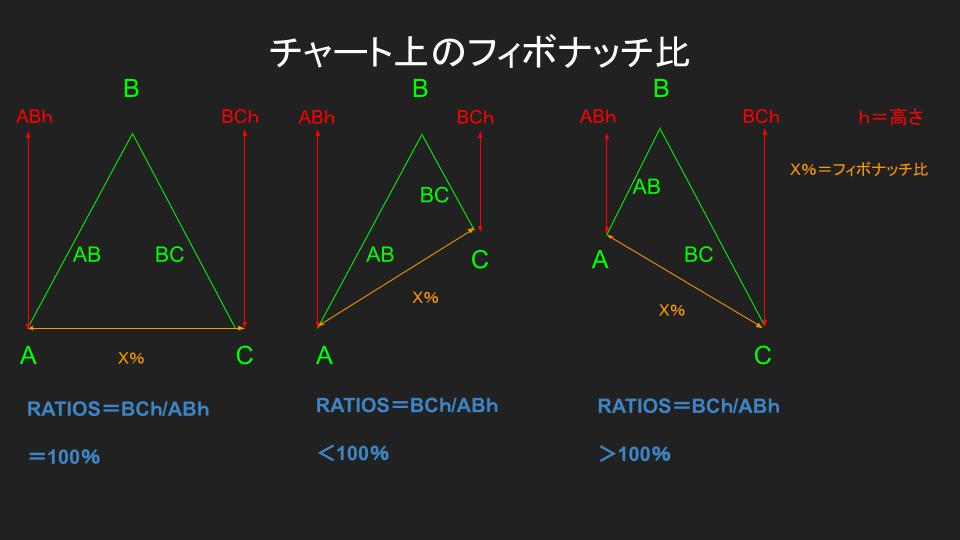
例えば、上記の画像で見てみると価格帯Aの位置から価格帯Bを通って価格C帯まで価格が変動している3つのパターンがありますよね。
価格Aから価格Bの上昇トレンドをABセグメント、価格Bから価格Cの下降トレンドをBCセグメントと定義します。
更にABセグメントの高さをABh、BCセグメントの高さをBChとしています。
ここで再度確認ですが、フィボナッチ比とはある値から前回の値で割った比率のことを指していました。
よってBChの値からABhの値で割ることで、価格Aから価格Cまでのフィボナッチ比率がわかるという訳です。
ハーモニックパターン
それでは、実際にどんなハーモニックパターンがあるのか確認していきましょう。
チャート上でフィボナッチ比率を当てはめる方法を理解した所で、この一連の価格変動はパターン化されていることに注目します。
過去のチャートでもこのフィボナッチ比率が使用されているチャートパターンが何度も登場します。
つまりフィボナッチ比で形成されるチャートパターンというものが存在するという訳です。 そしてフィボナッチ比とは、人間にとって無意識に働きかける調和された比率です。
フィボナッチ比によって形成されたものは人間の意識が集中しやすく、チャート上で意識されたポイント(価格帯)はどうなるでしょうか。
そうです。
その価格帯は強いサポートやレジスタンスになり、反発する可能性が非常に高くなります。
さらにハーモニックパターンは、決められた比率を使用するため反発されやすいポイントを事前に把握できるというメリットがあるんですね。
という事は、ストップロスもかなり抑え込むことが出来るので、リスクリワードが良い手法となります。
さて、ハーモニックパターンには強気相場と弱気相場でのパターンが存在します。 ここでは、11種類のハーモニックパターンを紹介していきます。
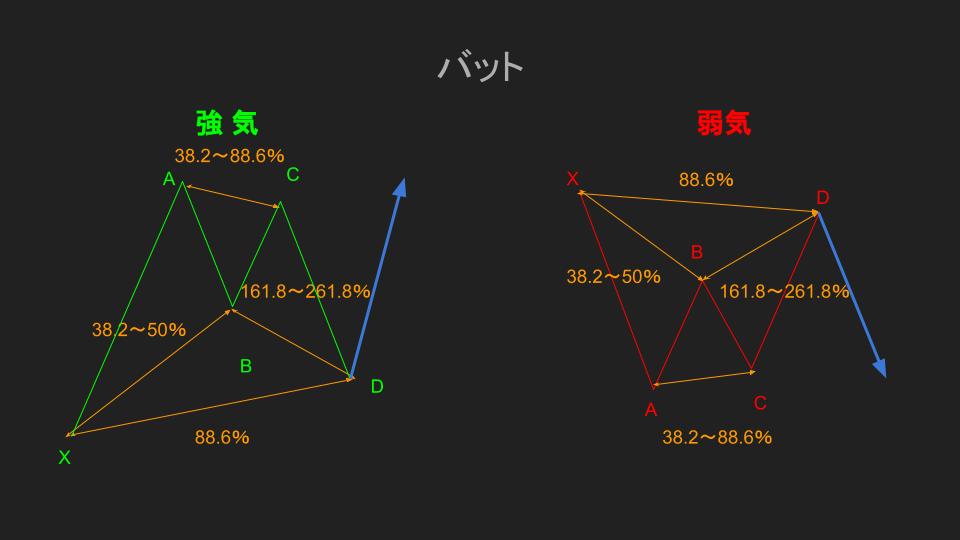
バット
基本ハーモニックパターンの一つです。
ここで注意してほしいのは、上記の比率はあくまでも参考程度に捉えておいてください。
バットの特徴はコウモリの形に似ているからだと言われています。
XAセグメントの安値と高値を更新できずに、D点の価格帯まで落ちた時に反発するパターンです。
このバットを形成するルールとして、
- B点:XAセグメントからのリトレイスメント38.2~50%
- C点:A点を抜けないこと(ABセグメントからのリトレイスメント38.2~88.6%)
- D点:XAセグメントからのリトレイスメント88.6%かつX点を超えないこと(BCセグメントからのエクステンション161.8~261.8%)
この3つのルールを満たしていることが条件となります。
ALTバット
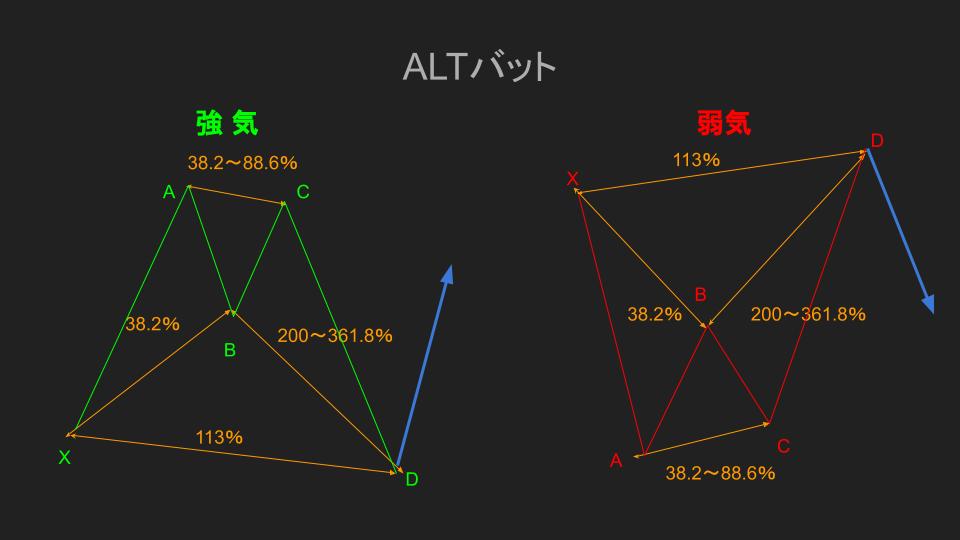
バットの派生形パターンになります。
ALTとはオルタネートの略語で代替という意味を持ちます。
この派生形のバットは、XAセグメントの安値を更新している所が特徴です。
このALTバットを形成するルールとして、
- B点:XAセグメントからのリトレイスメント38.2%
- C点:A点を抜けないこと(ABセグメントからのリトレイスメント38.2~88.6%)
- D点:X-Aからのエクステンション113%かつX点を超えること(B-Cからのエクステンション200~361.8%)
この3つのルールを満たしていることが条件になります。
バタフライ
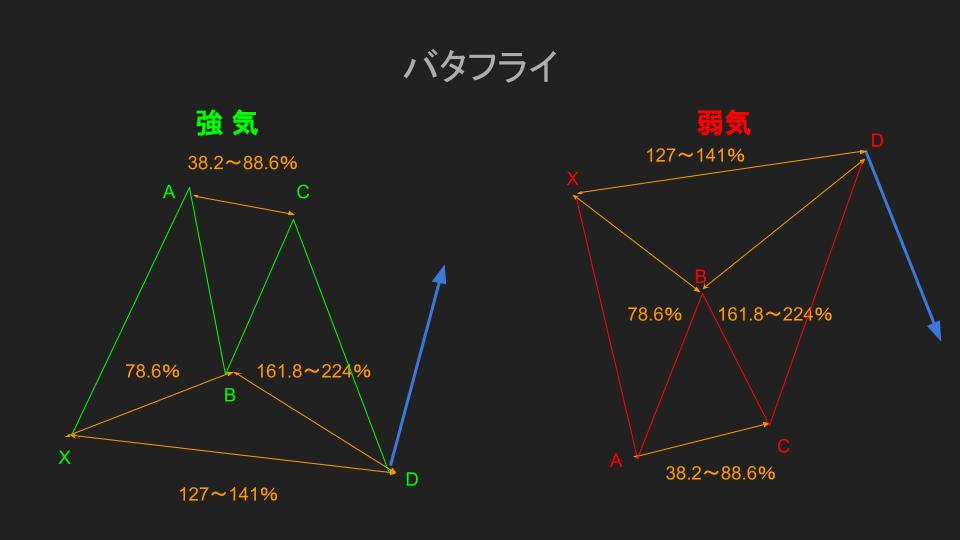
基本ハーモニックパターンの一つです。
この形の名前の由来は蝶に見立てているからなんですが、このバタフライの特徴として、XAセグメントに対してのリトレースメント(ABセグメント)が深いのが分かると思います。
このバタフライを形成するルールとして、
- B点:XAセグメントからのリトレイスメント78.6%
- C点:A点を超えないこと(A-Bからのリトレイスメント38.2~88.6%)
- D点:XAセグメントからのエクステンション127~141%かつX点を超えること(BCセグメントからのエクステンション161.8~224%)
この3つのルールを満たしていることが条件となります。
クラブ

基本ハーモニックパターンの一つです。
このクラブは、カニのハサミがどちらかが大きいことから、チャートでも垣間見ることが出来ます。
このクラブを形成するルールとして、
- B点:XAセグメントからのリトレイスメント38.2~61.8%
- C点:A点を抜けないこと(ABセグメントからのリトレイスメント38.2~88.6%)
- D点:X点を超えること(XAセグメントからのエクステンション161.8%)かつ(BCセグメントからのエクステンション261.8~361.8%)
B点だけで見ると、38.2~61.8%と幅が広いため他のハーモニックパターンと判別がつかないのと、D点がX点を超えてようやくALTバットかクラブかという判別になります。
ディープクラブ
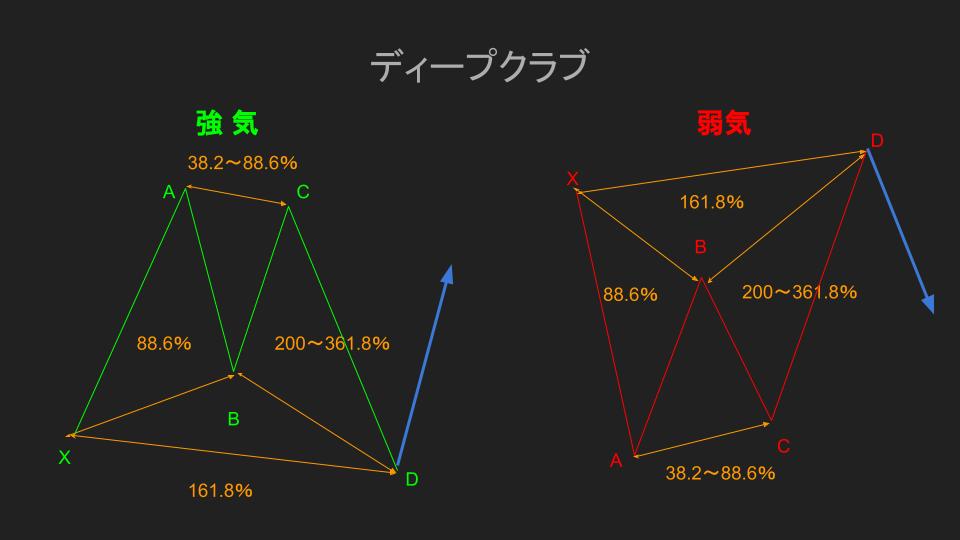
クラブの派生形パターンになります。
基本パターンのクラブと比べてもハサミの部分の切れ込みが深くなっているのが分かると思います。
このディープクラブを形成するルールとして、
- B点:XAセグメントからのリトレイスメント88.6%
- C点:A点を抜けないこと(ABセグメントからのリトレイスメント38.2~88.6%)
- D点:X点を超えること(XAセグメントからのエクステンション161.8%)かつ(BCセグメントからのエクステンション200~361.8%)
ディープクラブの特徴はB点が88.6%ということです。
このB点が65%を超えた時は、バタフライ(78.6%)かディープクラブを考慮する形になります。
ガートレー
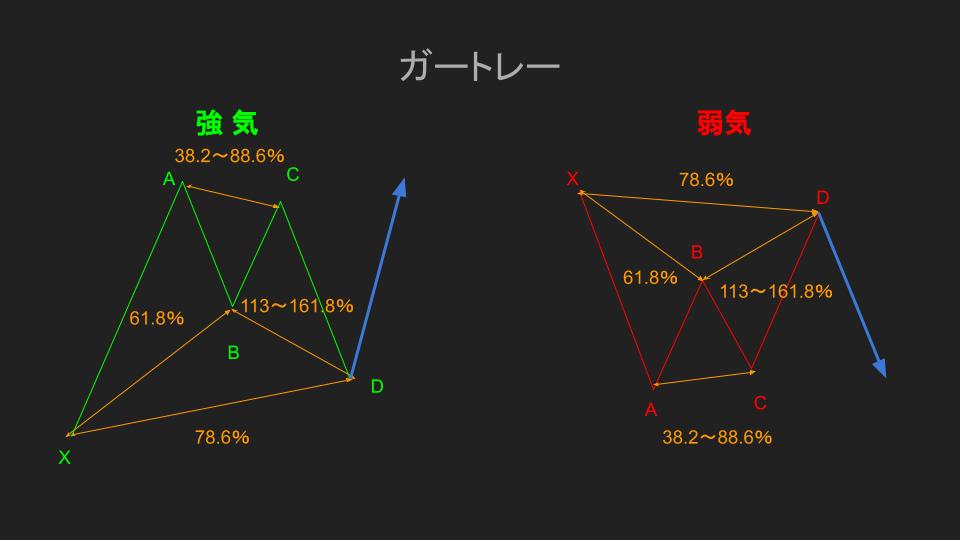
ガートレーは基本パターンの一つです。
H・M・ガートレー氏が最初に発見され、命名されたあとにスコット・カーニー氏によって詳しく定義されたパターンで、大きな流れからトレンドが新たに形成される時にかなりの頻度で起きているパターンだと言われています。
ガートレーを形成するルールとして、
- B点:XAセグメントからのリトレイスメント61.8%
- C点:A点を抜けないこと(ABセグメントからのリトレイスメント38.2~88.6%)
- D点:X-Aからのリトレイスメント78.6%かつX点を超えないこと(B-Cからのエクステンション113~161.8%)
特徴としては、XAセグメントで見た時に、高値も安値も更新していなく、XAセグメントの中で繰り返す可能性があります。
また、B点の61.8%はフィボナッチ比率の中でも意識されやすいので、反転していくエネルギーが強いことも特徴と言えます。
つまり、B点を超えて上昇の兆しを見せたとしても、長くは上昇できず、A点を超えることが出来ないので、再度反発していくといったニュアンスを持つと理解しやすいと思います。
シャーク
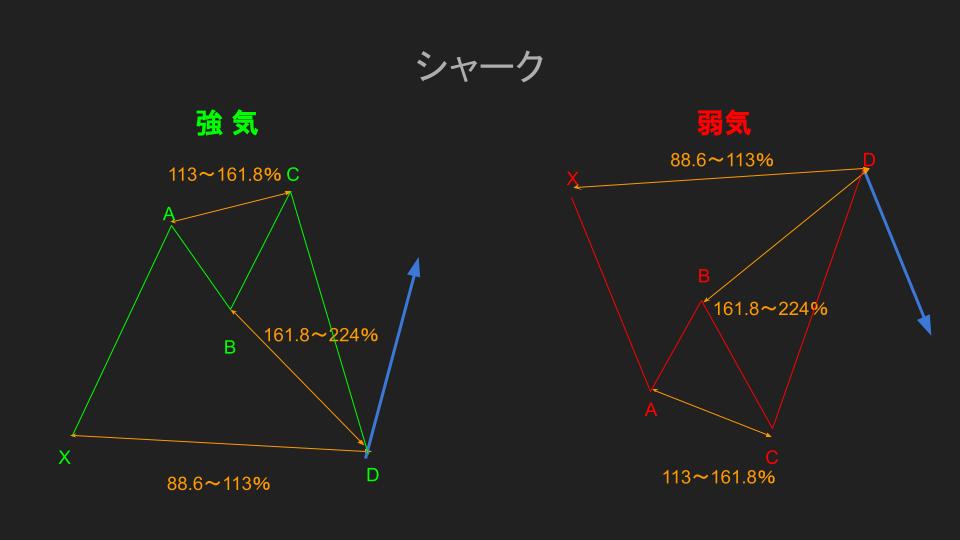
基本パターンで絶対ルールとして、C点はA点を超えてはならないとありましたよね。
でも実際に超えてしまうパターンも必ず存在します。
今回は、このC点が超えてしまった場合のハーモニックパターンをご紹介します。
ここではシャークを解説していきますが、形成するルールとして、
- B点:XAセグメントからのリトレイスメントは特段決まりはない
- C点:A点を抜けること(ABセグメントからのリトレイスメント113~161.8%)
- D点:XAセグメントからのエクステンション113~161.8%かつX点を超えること(BCセグメントからのエクステンション161.8~224%)
このシャークの特徴はまず、B点のリトレースメントは特段決まりがない事です。
今までXAセグメントに対してのリトレースメントB点を分析していましたが、シャークでは考える必要がありません。
むしろ、C点がA点を超えた時点でシャークパターンを予測します。
更に反転ポイントのD点を予測するには、BCセグメントに対してのエクステンションの比率のみを使うのがポイントです。
サイファー
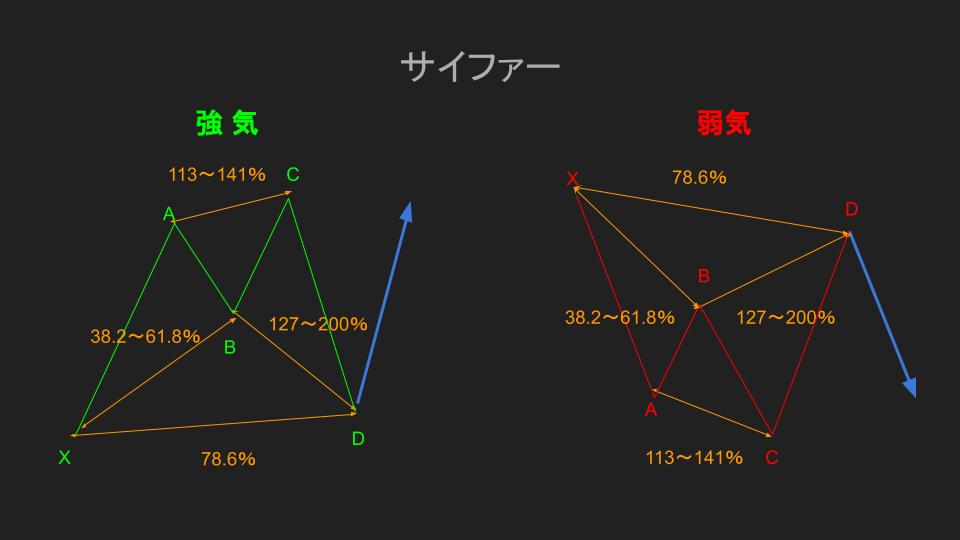
サイファパターンはダレン・オグレスビーによって発見され、シャーク同様にC点はA点を超えているという点が特徴です。
サイファーとは暗号という意味で、アラビア語で0という意味です。
元々、輪という意味を持つため、その形に由来を持つと言われています。
サイファーを形成するルールとして、
- B点:XAセグメントからのリトレイスメント38.2~61.8%
- C点:A点を抜けること(ABセグメントからのエクステンション113~141%)
- D点:XAセグメントからのリトレイスメント78.6%かつX点を超えないこと(BCセグメントからのエクステンション127~200%)
特徴としては安値や高値更新に失敗するするも、それを追い上げようとする動きがありますが、結局フィボナッチ比率のエネルギーによって引き戻されます。
まさに今までの更新の期待を0にするかのような動きですね。
5-0
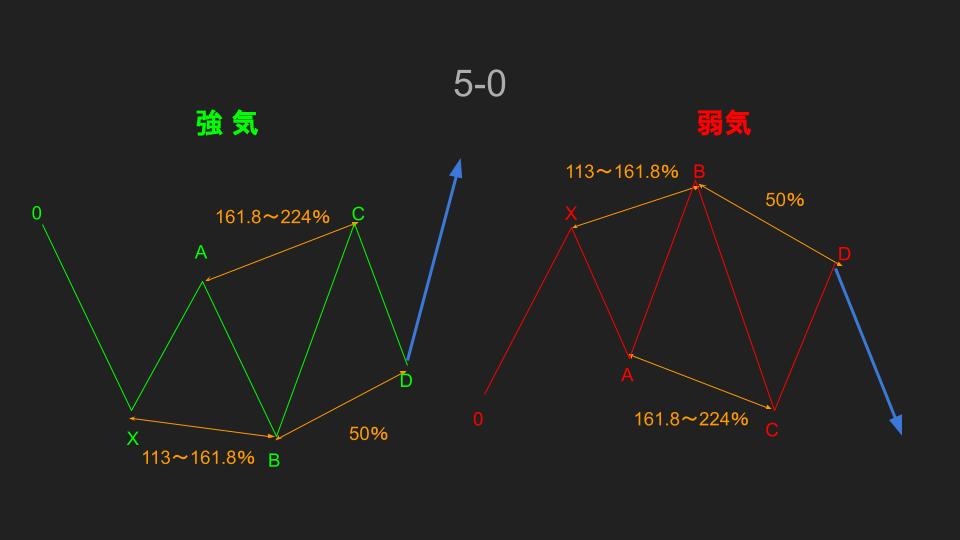
次は特殊パターンのハーモニックパターンの紹介になります。
今回は5-0(ファイブゼロ)というもので、BCセグメントのリトレースメントが50%であることからだという由来があります。
この5-0を形成するパターンとして、
- B点:XAセグメントからのエクステンション113~161.8%
- C点:A点を抜けること(ABセグメントからのエクステンション161.8~224%)
- D点:XAセグメントからのリトレイスメント50%
特徴はD点はXAセグメントのリトレースポイントが50%と決まっているため、狙いやすいです。
またシャークパターンのX点を超えたものと同じ形になるので、D点がX点を超えた動きの後にリトレースメントが50%なら5-0パターンになります。
AB=CD
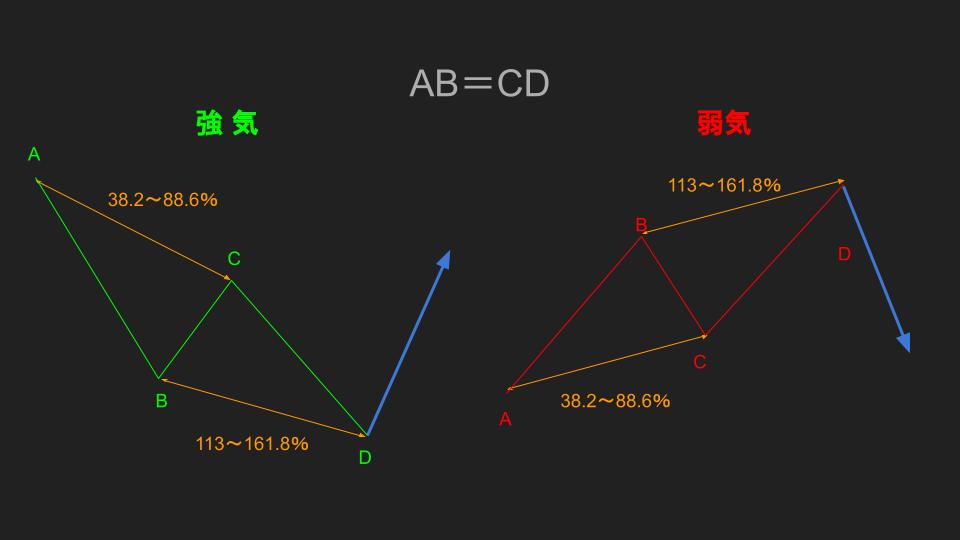
基本的にAB=CDとは、N波動の推進波ABと調整後の推進波CDが同じ幅になるということです。
このAB=CDパターンはかなり応用が利くので、他のテクニカル分析にも使えるのが特徴です。
例えば、
- ハーモニックパターン
- N波動理論
- チャネルライン
このように、かなり汎用性の高いパターンですが、今回はハーモニックパターンとして一部解説していきます。
- C点:ABセグメントのリトレースメント38.2~88.6%
- D点:BCセグメントのエクステンション113~261.8%
スリードライブ
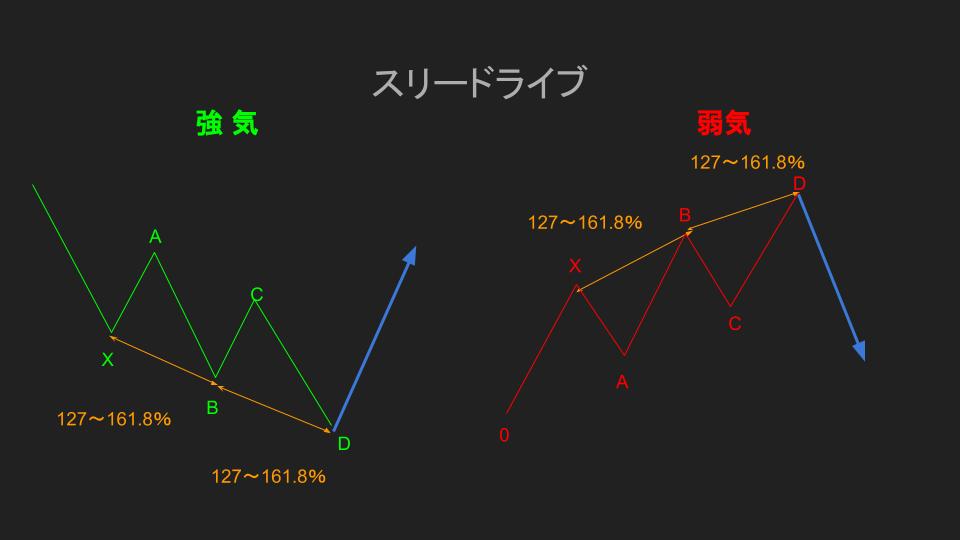
最後にスリードライブについてご紹介します。
このスリードライブが発生するのは、上昇や下降が終結しようとするときに発生しやすいパターンです。
チャートパターンのウエッジに近いのでなじみ深いのではないでしょうか。
そんなスリードライブの形成のルールを確認すると、
- B点:X-Aからのエクステンション127~161.8%
- D点:B-Cからのエクステンション127~161.8%
この2つのルールを満たしていることが条件となります。
ハーモニックパターンを使用するにあたっての注意点
ハーモニックパターンの基本形と派生形、そして特殊パターンの紹介を終えましたが、このハーモニックパターンを使用する上で注意しなくてはならない事があります。
上記のような形を見つけて即エントリーという訳にはいかず、どうゆう根拠でハーモニックパターンを当てはめているのか知る必要があるんですね。
そうでないと、折角学んだパターンを活用できず、資金もマインドもすり減らしてしまいます。
ハーモニックパターンは全て縦軸の比率のみで表している
このハーモニックパターンは、縦軸の価格変動によってフィボナッチ比率を導き出し、あらゆるパターンを表しています。
実際、横軸(価格の距離)はそれほど重要視されていないんですね。
横軸が重要視されていないとどうなるかと言いますと、 教科書通りのキレイなパターンは、実際のチャートでは形が歪むことがあります。
基本的に各セグメントまでの価格変動時間は、同じ持続時間でると想定されていますがそうではない可能性があります。
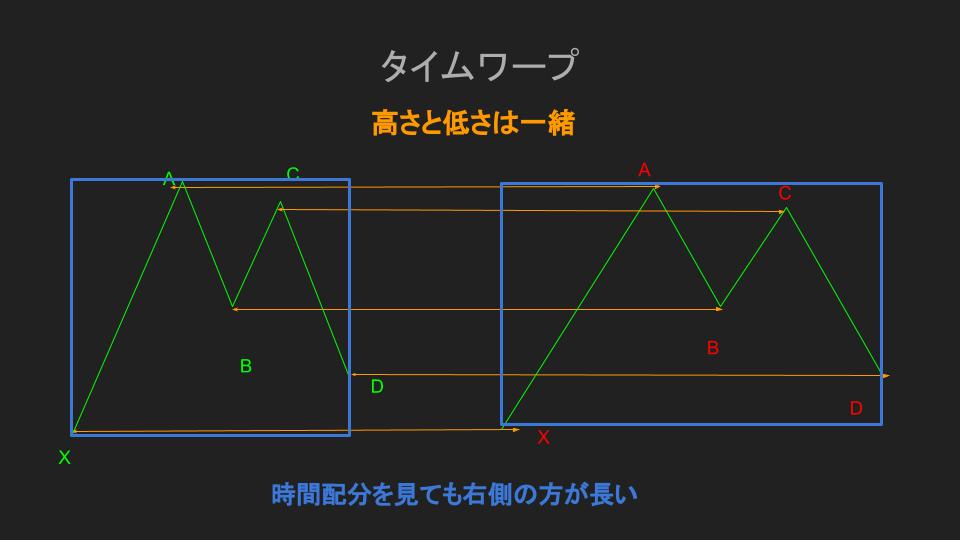
よって、ハーモニックパターンは無限の異なる形状をもつことになります。
エントリータイミングを教えてくれるわけではない
この手法はあくまでも各ハーモニックパターンに示された最適な調和比率が意識されているかどうかを示すだけで、最適なエントリータイミングを示すわけではありません。
エントリータイミングは他のテクニックを使ってタイミングを図る必要があります。
レシオ・コンバージェンス
今までのハーモニックパターンを見てみると、フィボナッチ比率が広範囲の場合と、特定の比率があるかと思います。
例えば、XAセグメントのリトレースメントだけで見ても、各ハーモニックパターンを見てみても断定することが出来ません。
更に、C点がA点を超えるか超えないかでもパターンが分岐しますよね。
逆に考えれば、セグメントの比率が確定すればするだけ、パターンが絞られていくことになります。
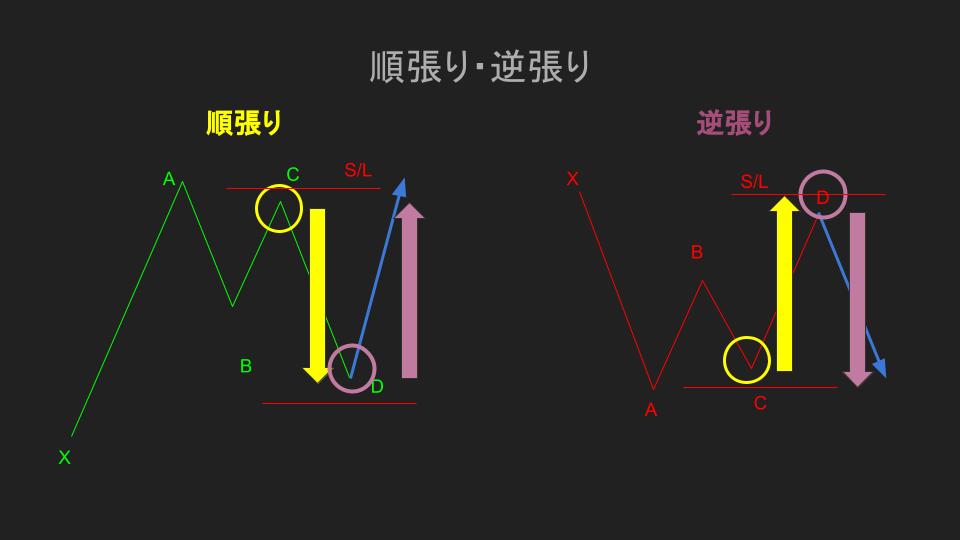
オススメなのは、D点を予測して逆張りを狙う方法と、C点が確定してからパターンに沿ってリスクリワードを設定して順張りする方法です。
この早見表は、左から順に絞り込むための早見表です。
使い方は左のXAとは、XAセグメントのリトレースメントのB点までの比率を表しています。
38.2~61.8%までの範囲をオレンジに区別してますので、この範囲にある間はパターンが定まりませんが、それを超えると今度は、紫に区別している比率になります。
言い換えれば、紫の範囲までくれば、パターンが絞れます。
BCというのはBCセグメントのエクステンションのD点が、右の数字まで伸びることを指しています。
例えば、XAリトレースメントが40%、C点がA点を超えて、D点がX点を超えず、BCエキステンションが88.6%付近ならバットという形になります。
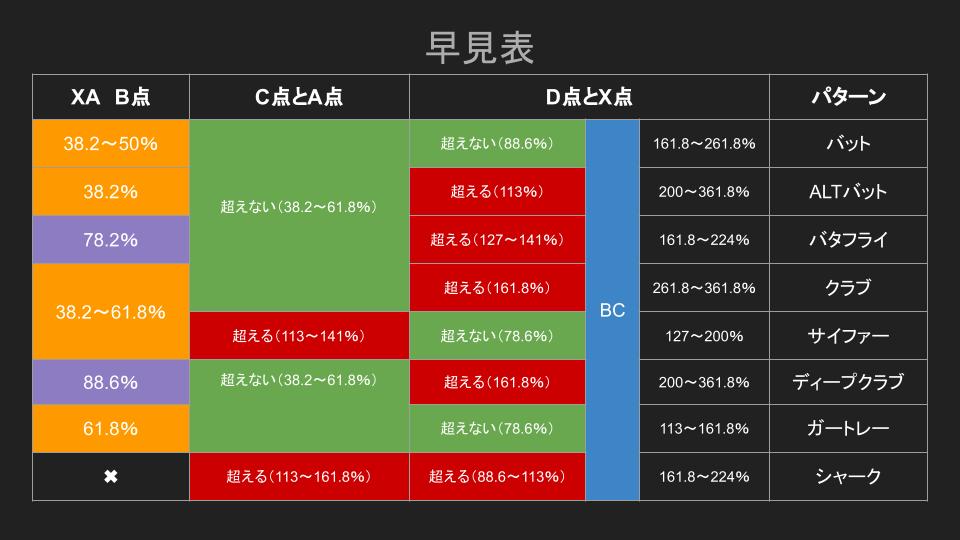
こんな感じで、早見表を使ってみて下さい。
達成しなければならないルールを順に確認して、パターン構成に必要な比率が収束してきたら、C点からの順張りか、D点からの逆張りを狙うといいでしょう。
トレード手法
- 上記の早見表で、価格反転ゾーン(PRZ)や、反転ラインに到達するまで待つ
- 他のテクニックを使って、反転を確認する(テクニックはMAやオシレータといったラグが発生するものは避ける)
- 自分の根拠が崩れる所にストップロスを設置する
- リスクリワードを3~5:1に設定する
この辺りは動画取れ次第随時アップしていきます。
メリット
- MA(移動平均線)のようなテクニカル分析のように計算式を必要としないので、このハーモニックパターンは縦軸の比率のみを扱い、フィボナッチ比率を当てはめているだけなので分析のラグが派生しない
- 反発ラインを事前に予測できるため、リスクリワードが良い
- 比較的新しい分析方法のため、現在でも研究が進められ、実際に新しいパターンが見つかっている
デメリット
- 実際のチャート内では、タイムワープ問題や無限とも言えるパターンの種類により、ハーモニックパターンを見つける事が容易ではない
- あくまでも価格変動が反転に最適なゾーン内にあるかどうかを示すだけで、エントリータイミングは正確には教えてくれない
- フィボナッチ数列が金融市場でも最適化されているという仮定での分析方法
- 科学的根拠で証明されている訳ではなく、自己充足予言が見られる
※自己充足予言とは、投資の話でいうと「ある手法が機能するのは、科学的根拠があるからではなく、他のトレーダーが機能すると信じ始めるから」といった根拠の無い見立てや思い込みを持つと人は無意識にその予言に沿った行動をとるために、もともとは実現する予言が現実のものとなる現象
まとめ
今回はハーモニックパターンについて解説しました。
ハーモニックパターンとは、黄金比でも有名なフィボナッチ比率を使用した一種のチャートパターンになります。
人は造形の美しさに無意識に求める傾向があるため、チャートパターンにもその心理が働くという事でした。
また、チャートパターンには基本形、派生形、特殊パターン、新種パターンに分ける事ができます。
基本形では、バット、バタフライ、クラブ、ガートレー 派生形では、ALTバット、ディープクラブ、
特殊パターンは、5-0、スリードライブ
新種パターンは、サイファー、シャークとなります。
AB=CDは厳密にいうと、汎用性の高いチャートパターンなので、ハーモニックパターンにも当てはまるといった感じです。
次にハーモニックパターンは、実際のチャート上では教科書通りに示すことはなく、横軸の価格変動時間は考慮してないという点です。
更には、エントリータイミングは正確に教えてくれるものではなく、価格反転ゾーン(PRZ)や価格反転ラインを示すものなので、エントリータイミングは別の手法(計算式を必要としないもの)を合わせると効果的というお話をしました。
さていかがだったでしょうか。
今回も長くなってしまいましたが、電子書籍化するために色々と試している最中なので、もうしばらくお待ちください。
それでは今回は以上です。
また次の記事でお会いしましょう。
それでは。


